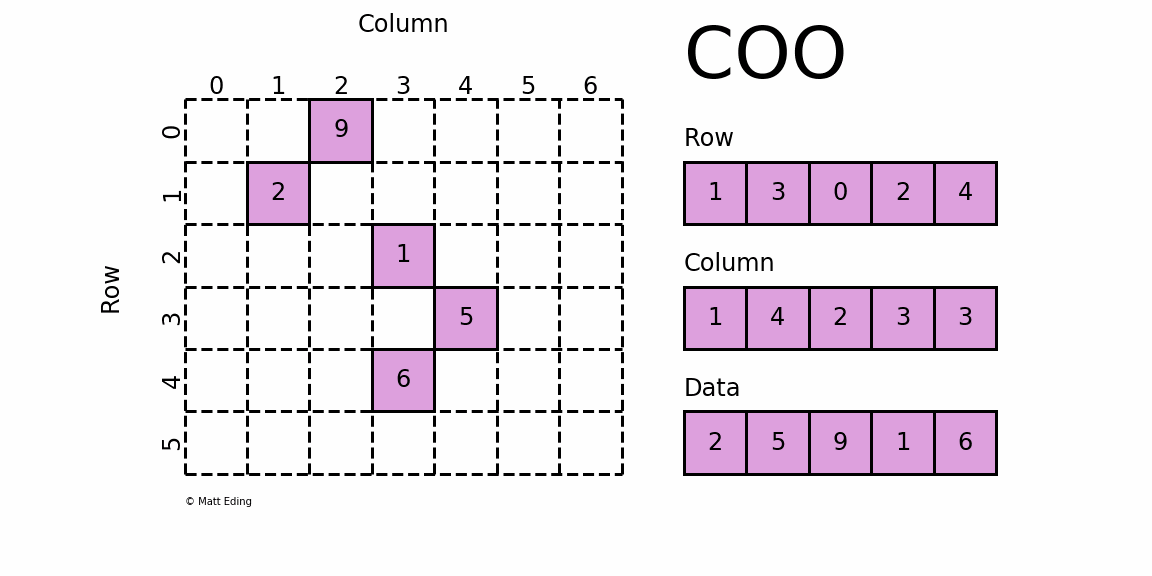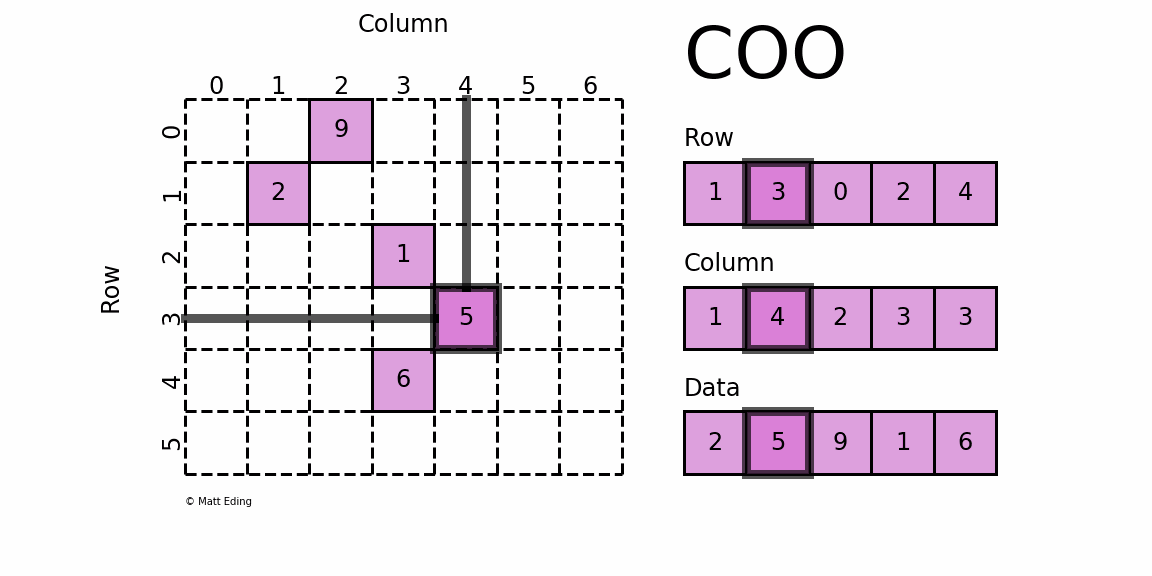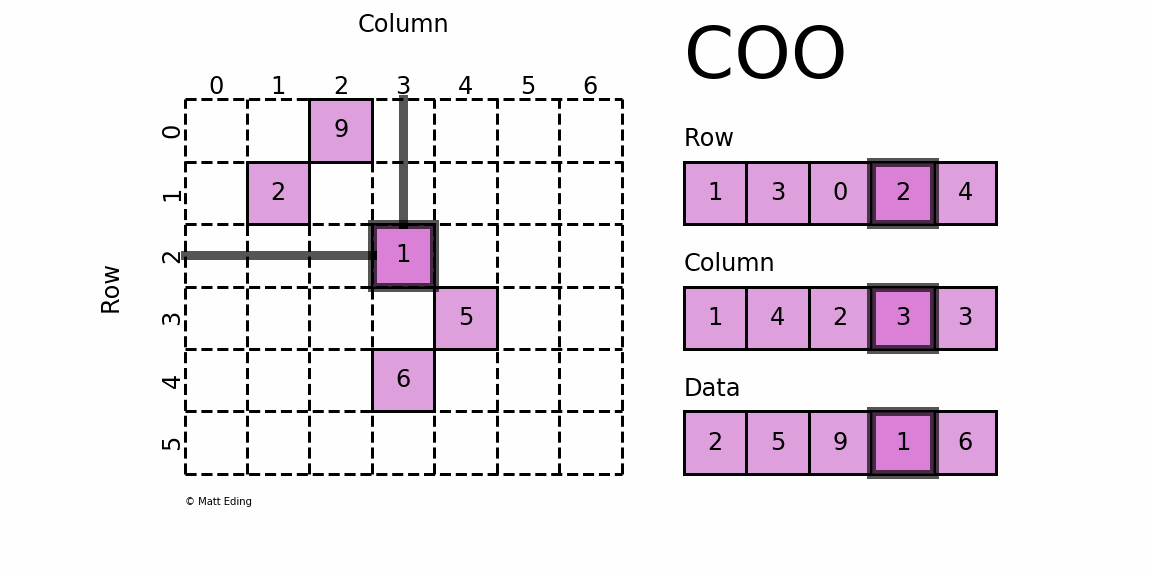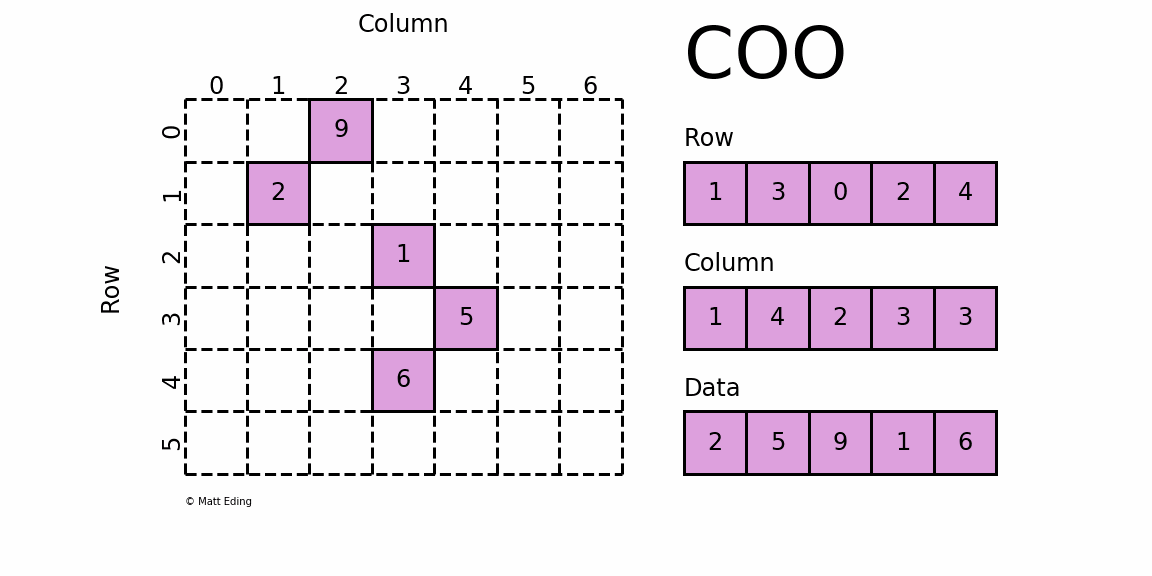
Addition Of Sparse Matrix Algorithm
For i 0. L x b are sparse x b for j 0 to n 1 do if x j 6 0 for each i j for which l ij 6 0 do x i x i l ijx j non-optimal time On jbj f where f op count problem.
 Sparse Matrix Computation An Overview Sciencedirect Topics
Sparse Matrix Computation An Overview Sciencedirect Topics
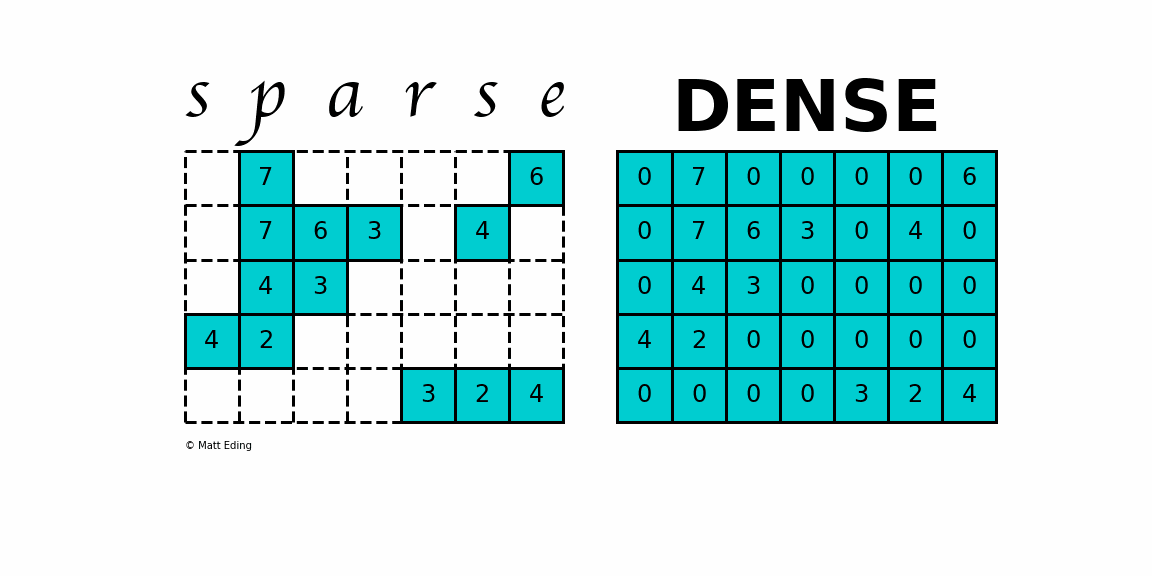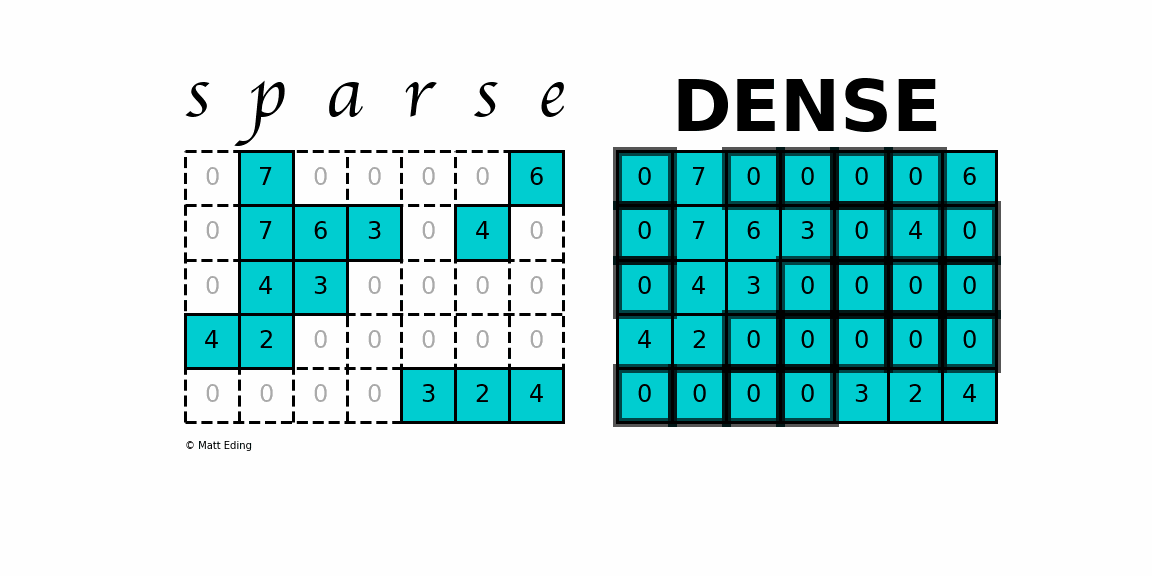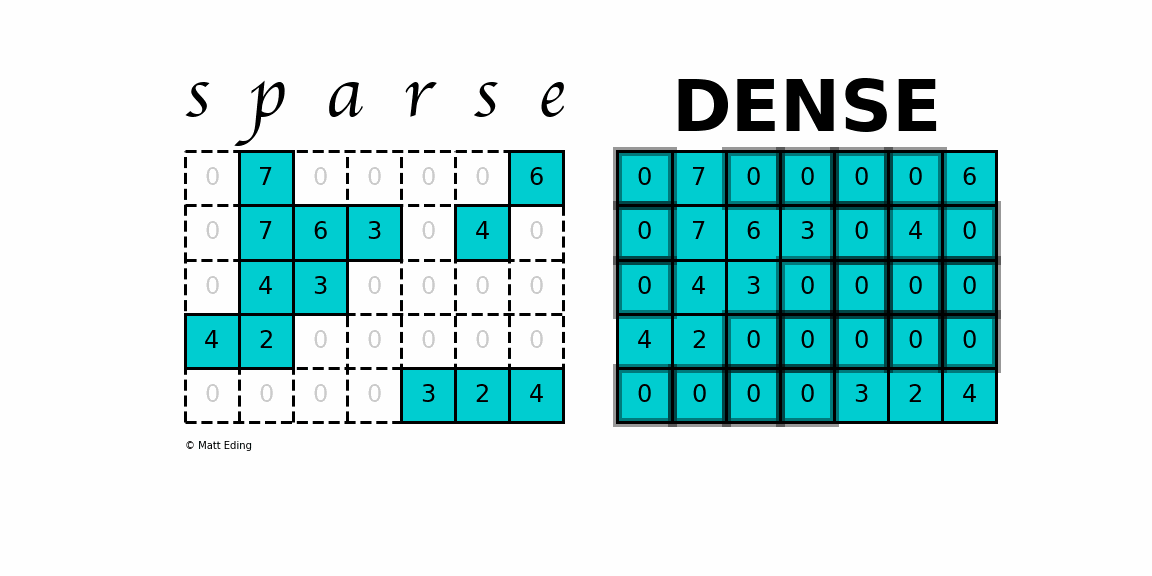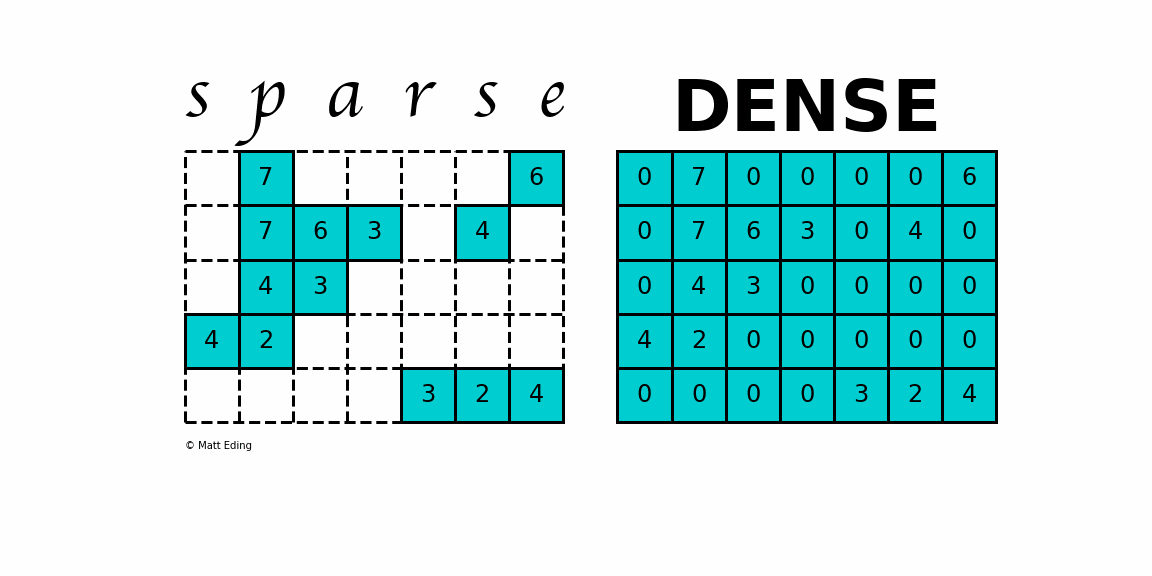
A sparse matrix is a matrix or a 2D array in which majority of the elements are zero.

Addition of sparse matrix algorithm. The Collection is widely used by the numerical linear algebra community for the development and performance evaluation of sparse matrix algorithms. It allows for robust and repeatable experiments. Matrix multiplication follows distributive rule over matrix addition.
Implementing Sparse Matrices for Graph Algorithms thenonassignedtriplesegforB. CUSPARSE has some routines that can operate on two operands that are both sparse matrices for addition and multiplication. Scalar multiplication is compatible with multiplication of matrix.
This code takes each index-value pair iv in the sparse row multiplies v with the i value of x and sums the results. The work and depth is easily calculated using the performance rules. Given two sparse matrices Sparse Matrix and its representations Set 1 Using Arrays and Linked Lists perform operations such as add multiply or transpose of the matrices in their sparse form itself.
Set IA0 to 0. HttpsyoutubeCU3Hynyi81Q Sparse Matrix Transpose at 000500 Sparse Matrix Addition at 001100 Sparse Matrix u. Sumv xi.
K Athosearethetriples ij B ij where j k andfinallyconcatenatesthenonzerosinAtotheoutput. The computational bottleneck in such algorithms is the formation of the SMMV products. Operations on Sparse Matrices.
For example in the subspace iteration method used for solving for a few eigenvalues of a large sparse matrix A one forms the Rayleigh quotient projection matrix M STAS where A Rnnand S Rnpis a dense matrix with p n. For each case we obtain asymptotic improvement over existing algorithms. In addition the sparsity is visualized by the so-called covariance graph Chaudhuri Drton Richardson 2007.
The result should consist of three sparse matrices one obtained by adding the two input matrices one by multiplying the two matrices and one obtained by transpose of the first matrix. I i 1 for k RowPtri. This function performs following matrix-matrix operation.
In this matrix only 10 spaces are filled with non-zero values and remaining spaces of the matrix are filled with zero. In such an operation the result is the dot-product of each sparse row of the matrix with the dense vector. In particular our matrix multiplication algorithm is.
The NESL code for taking the dot-product of a sparse row with a dense vector x is. Intuitively the most suitable approach to cope with this problem is finding an estimate of the covariance matrix that is as sparse as possible since the sparsity leads to the effective reduction in the number of parameters. In the covariance graph each node presents a random variable in a random.
Robust because performance results with artificially-generated matrices. Where A B and C are mn sparse matrices defined in CSR storage format. SPARSIFY MATRIX Step 1.
Set M to number of rows in MATRIX Step 2. Set N to number of columns in MATRIX Step 3. λ AB λA B and A Bλ Matrix Multiplication Algorithm.
K k 1 resulti 0. For example consider a matrix of size 100 X 100 containing only 10 non-zero elements. In a naive way you multiply a values at row i in matrix A with a column in the matrix B and store the sum of the row operation as a result in the resultant matrix.
You can do sparse matrix - sparse matrix addition with CUSPARSE using the cusparsecsrgeam function. I 0 NNZ 0. Sparse matrix with C in Hindi follow.
In this paper we design massively parallel algorithms for sparse ma-trix multiplication as well as more general join-aggregate queries where the join hypergraph is a tree with arbitrary output attributes. Multiply matrix stored with Compressed Sparse Row method with vector dN for k 0. Declare variables and initialize necessary variables.
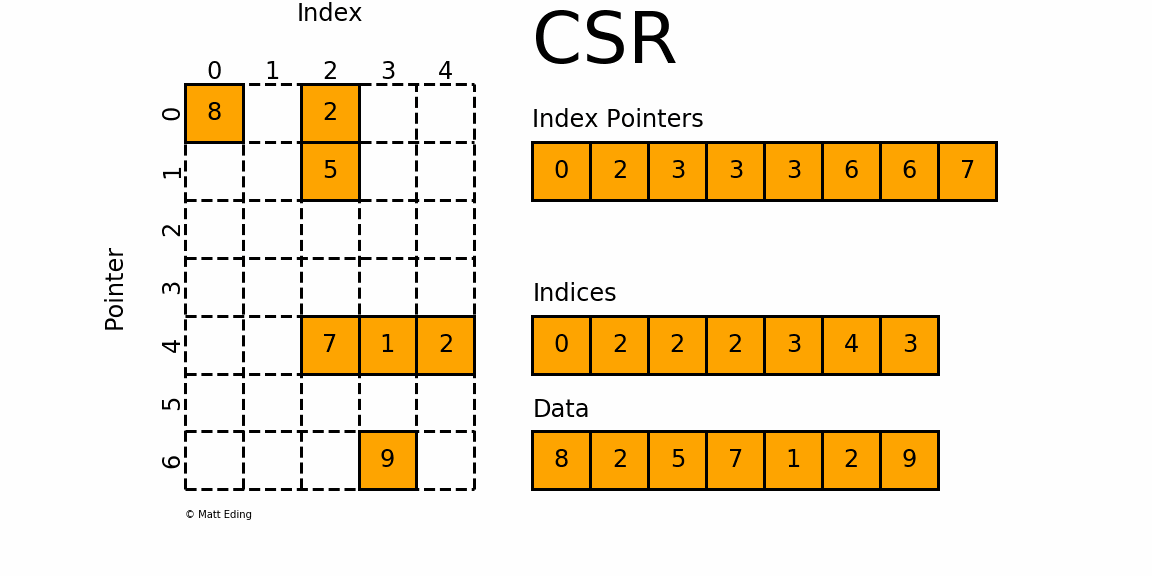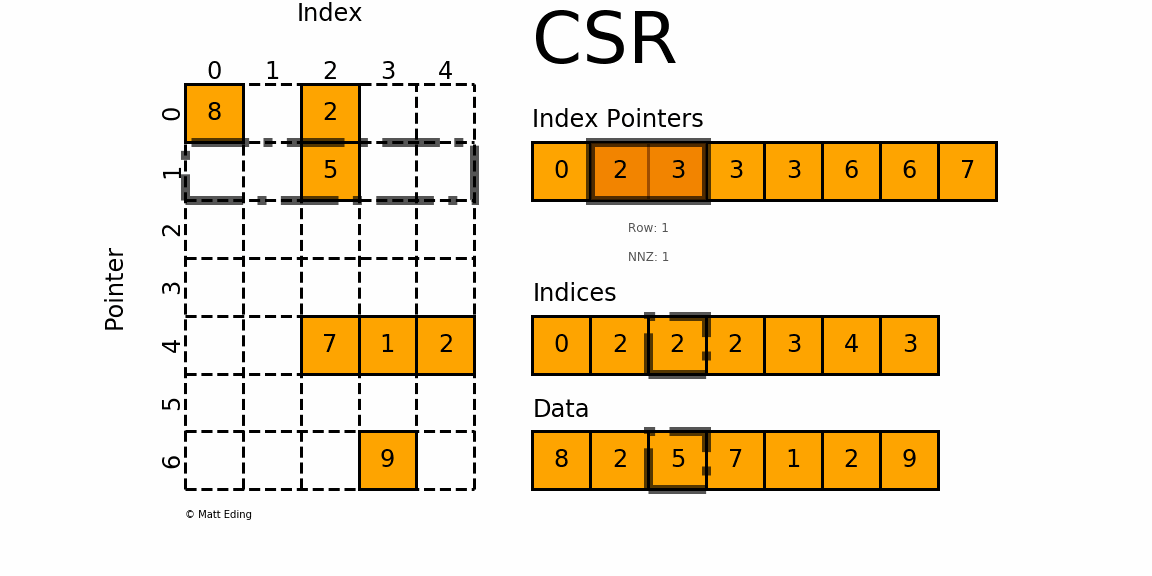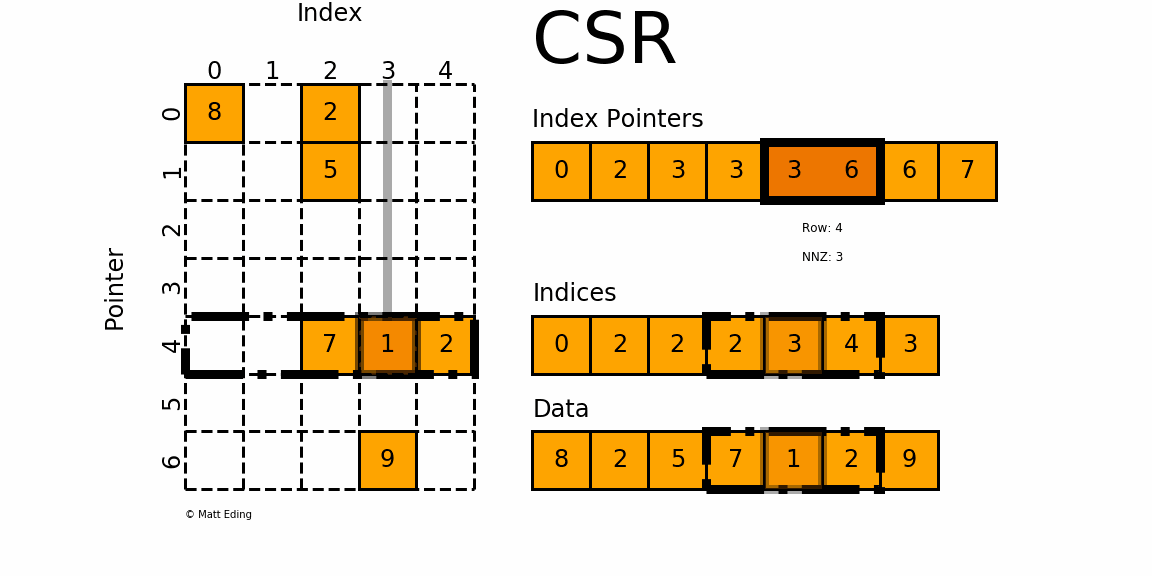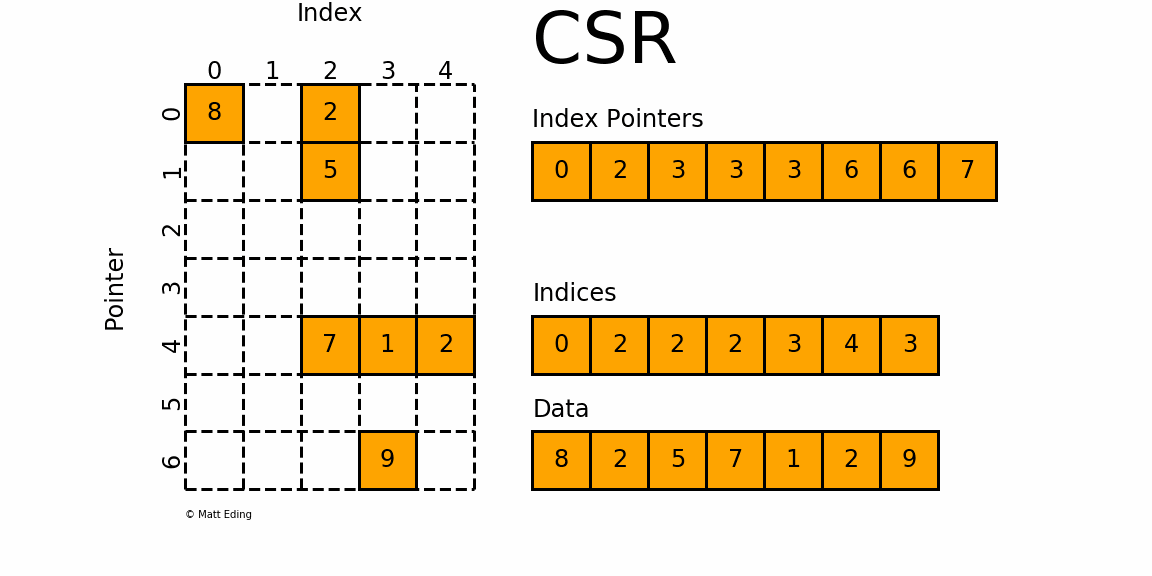
Declare A JA and IA. When a sparse matrix is represented with a 2-dimensional array we waste a lot of space to represent that matrix. A B C AB AC Right Distribution A B C AC AC.
K k 1 resulti resulti ValkdColk. Sparse matrix is a matrix which contains very few non-zero elements. Of rows and columns.
Matrix multiplication is a very simple and straightforward operation and one every computer science student encounters in the school at least once. Outer loop and the test for x j 6 0. Sparse matrix algorithms Solve Lx b with L unit lower triangular.
The SuiteSparse Matrix Collection formerly known as the University of Florida Sparse Matrix Collection is a large and actively growing set of sparse matrices that arise in real applications.
 Sparse Matrix Multiplication Description By Glyn Liu Medium
Sparse Matrix Multiplication Description By Glyn Liu Medium
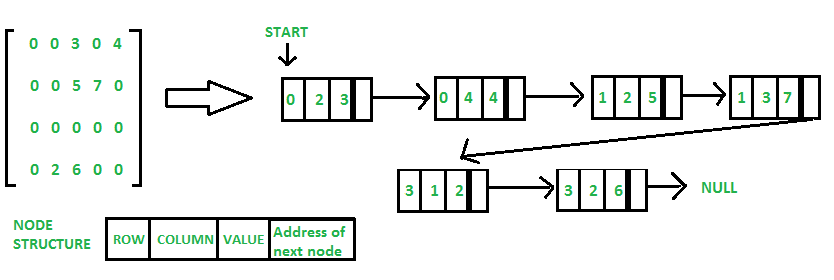 Sparse Matrix And Its Representations Set 1 Using Arrays And Linked Lists Geeksforgeeks
Sparse Matrix And Its Representations Set 1 Using Arrays And Linked Lists Geeksforgeeks
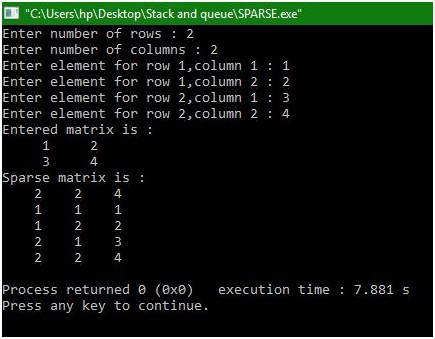 Sparse Matrix For 3 Tuple Method Using Array
Sparse Matrix For 3 Tuple Method Using Array
 Sparse Matrix And Its Representations Set 1 Using Arrays And Linked Lists Geeksforgeeks
Sparse Matrix And Its Representations Set 1 Using Arrays And Linked Lists Geeksforgeeks
 Sparse Matrix Vector Multiplication An Overview Sciencedirect Topics
Sparse Matrix Vector Multiplication An Overview Sciencedirect Topics
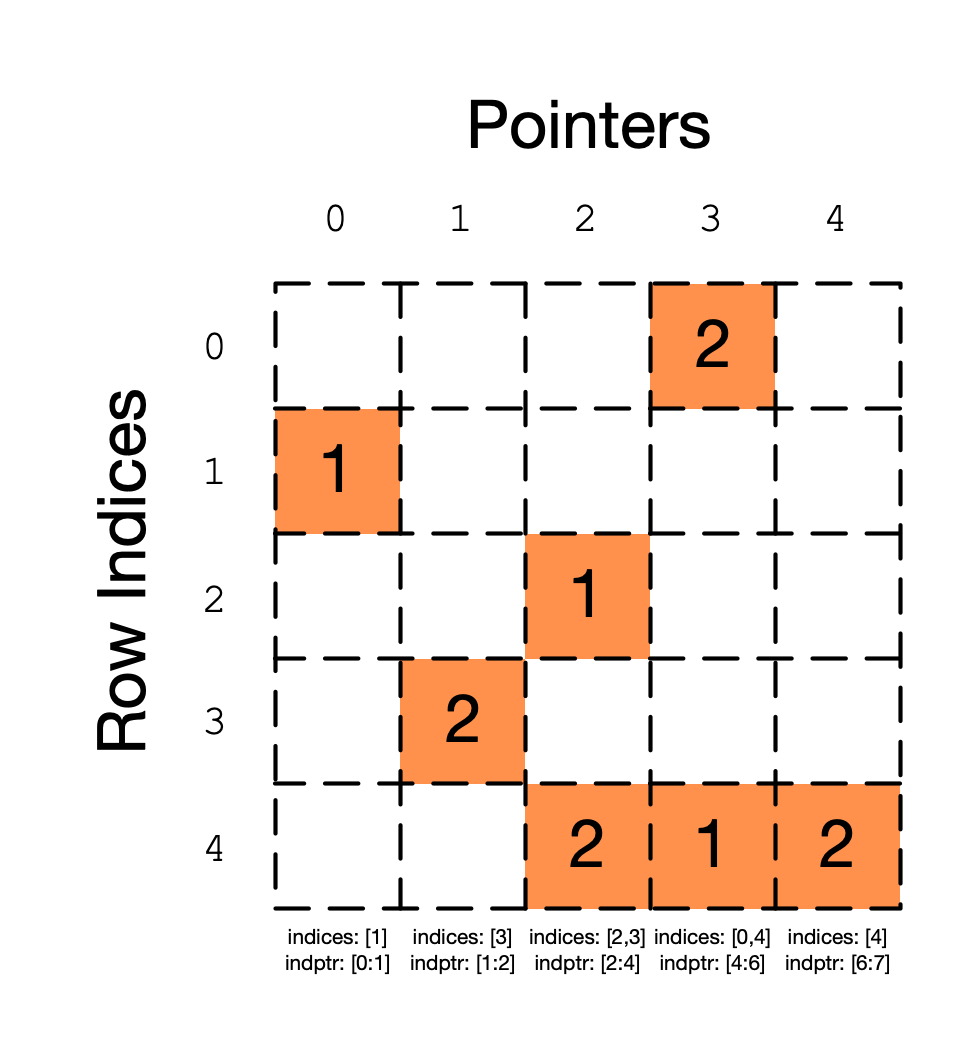 An In Depth Introduction To Sparse Matrix By Edward Cui The Startup Medium
An In Depth Introduction To Sparse Matrix By Edward Cui The Startup Medium
 Pseudocode Of The Csr Based Spmv Download Scientific Diagram
Pseudocode Of The Csr Based Spmv Download Scientific Diagram
 Addition Of Sparse Matrix Using Structure In C Triplet Form Stack Overflow
Addition Of Sparse Matrix Using Structure In C Triplet Form Stack Overflow
 Mca Free Full Text Practical Sparse Matrices In C With Hybrid Storage And Template Based Expression Optimisation Html
Mca Free Full Text Practical Sparse Matrices In C With Hybrid Storage And Template Based Expression Optimisation Html
 Mca Free Full Text Practical Sparse Matrices In C With Hybrid Storage And Template Based Expression Optimisation Html
Mca Free Full Text Practical Sparse Matrices In C With Hybrid Storage And Template Based Expression Optimisation Html
 Sparse Matrix And Its Representations Set 2 Using List Of Lists And Dictionary Of Keys Geeksforgeeks
Sparse Matrix And Its Representations Set 2 Using List Of Lists And Dictionary Of Keys Geeksforgeeks
 Sparse Matrix Algorithms Stanford June 2013 Tim Davis Youtube
Sparse Matrix Algorithms Stanford June 2013 Tim Davis Youtube
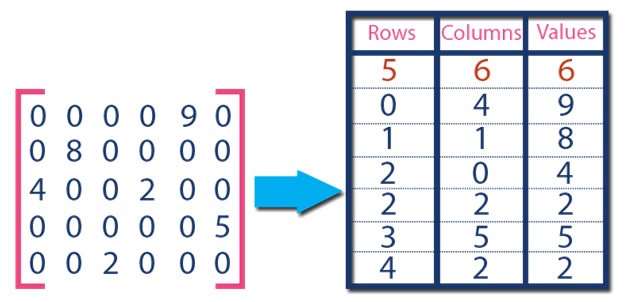 Sparse Matrix For 3 Tuple Method Using Array
Sparse Matrix For 3 Tuple Method Using Array
 Sparse Matrix Linked List Representation Data Structures Lec 25 Bhanu Priya Youtube
Sparse Matrix Linked List Representation Data Structures Lec 25 Bhanu Priya Youtube
 Mca Free Full Text Practical Sparse Matrices In C With Hybrid Storage And Template Based Expression Optimisation Html
Mca Free Full Text Practical Sparse Matrices In C With Hybrid Storage And Template Based Expression Optimisation Html